A análise de concorrentes é uma estratégia muito importante para que uma empresa se destaque no mercado. Em termos simples, essa prática se refere ao acompanhamento do posicionamento e das ações de outras empresas do mesmo ramo e pode ser muito útil para identificar riscos e oportunidades. Isso não é uma tarefa fácil, mas machine learning pode ser muito útil no processo!
Nesse texto, trataremos de um problema de predição de preços de venda do concorrente. Como resultado, teremos benefícios como saber quais são os melhores momentos de aplicarmos promoções, de forma a maximizar nossos resultados, e conhecer as tendências e sazonalidades do mercado. Para isso, utilizaremos séries temporais.
Séries temporais são conjuntos de dados ordenados no tempo, como dados de vendas e preços de ações, por exemplo. Em nosso problema, empregaremos alguns conceitos sobre séries temporais para realizar a predição de preços de abacate (em dólares). Apesar de ser um exemplo lúdico, ele pode servir como uma analogia para a análise de concorrência, como voltaremos a ver mais para frente.
Faremos esse exercício de predição utilizando Python (e algumas bibliotecas importantes) e um conjunto de dados disponível gratuitamente no Kaggle, que contém dados de venda de abacate nos Estados Unidos entre 2015 e 2018.
O código utilizado está disponível aqui.
Explorando o conjunto de dados
Antes de qualquer coisa, é importante entendermos sobre o conjunto de dados com o qual iremos trabalhar.
Abaixo podemos ver as cinco primeiras linhas do nosso conjunto de dados puro, sem nenhuma alteração.
A partir dessa visualização, chegamos a algumas conclusões:
- Existem muitos campos que não serão úteis para nossa análise. Apenas o preço e a data nos interessam (campos ‘Date’ e ‘AveragePrice’);
- Os dados não estão ordenados pela data;
- Carregando mais linhas do conjunto de dados, veremos também que existem vários valores para um mesmo dia, referentes a diferentes localidades. No nosso caso, seria mais interessante termos a média desses valores, para termos um valor geral.
Para resolver essas questões, iremos aplicar uma transformação no nosso conjunto de dados. Ficamos apenas com a média dos preços de abacate por dia, com distância de uma semana entre os dados.
Podemos dispor esse resultado em um gráfico, para melhor visualização:
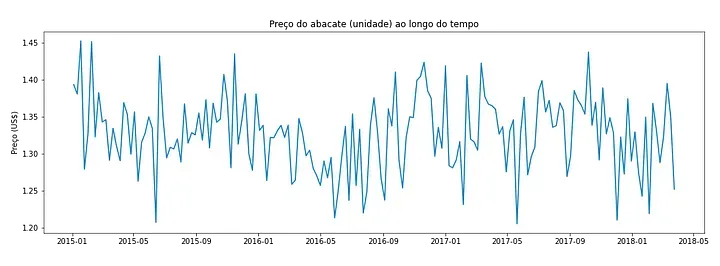
Agora que obtemos um dataframe limpo, podemos começar a pensar nas predições!
Separando a base de treino
Como em qualquer projeto envolvendo predições, é interessante que o conjunto de dados seja dividido entre uma base de treino e uma base de teste, para validarmos a eficácia do modelo.
Então, iremos formar uma base de treino com os 152 primeiros valores do nosso conjunto inicial (aproximadamente 90% do total dos dados) e o restante deixaremos em uma base de teste.
A seguir, podemos ver o resultado gráfico dessa separação.
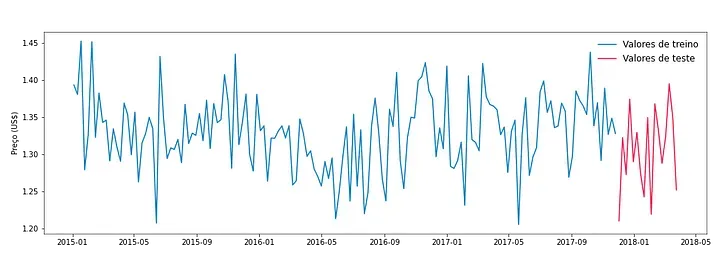
Analisando a série temporal
As séries temporais possuem diversas características que podem afetar a modelagem, como a sazonalidade, a tendência e a estacionariedade. Se elas forem presentes no conjunto de dados, será necessário fazer alguns ajustes antes de aplicar a modelagem.
Um exemplo dessas características é a tendência do aumento de preço com o lançamento de um novo produto. Além disso, notamos a sazonalidade no aumento das vendas do varejo nos períodos próximos à datas comemorativas, como o final de ano.
Voltando para a nossa análise, não conseguimos avaliar essas características no nosso conjunto de dados apenas com a representação gráfica gerada anteriormente. Então, utilizaremos o recurso visual da decomposição sazonal e o teste de Dickey-Fuller, que nos indicará estatisticamente se nossa série é estacionária ou não. Para isso, utilizaremos as funções seasonal_decompose() e adfuller() da biblioteca statsmodels.
Abaixo, temos a decomposição sazonal do nosso conjunto de dados. Nesses gráficos, conseguimos observar tanto a tendência quanto a sazonalidade da série.
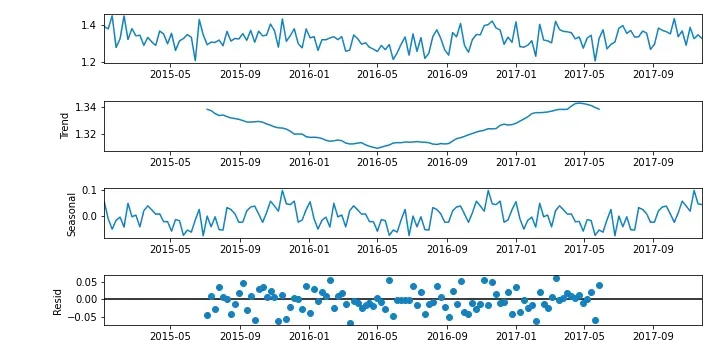
Observando a figura anterior, é possível notar uma pequena tendência de queda e vemos uma leve sazonalidade também. No entanto, é importante termos resultados mais objetivos e diretos para analisar se nossa base está adequada para a modelagem.
Para isso, utilizaremos o teste de Dickey-Fuller. Se obtermos um p-value inferior ao nível de significância adotado, rejeitamos a hipótese de que a série possui raiz unitária e, portanto, temos que ela é estacionária.
Teste Dickey-Fuller: -4.163590
p-value: 0.000759
Valores críticos:
1%: -3.4753
5%: -2.8813
10%: -2.5773
Esses resultados nos mostram que, mesmo a um nível de significância de 1% (o menor dos mais comumente utilizados), ainda rejeitaremos a hipótese da raiz unitária. Deste modo, concluímos que o conjunto de dados é estacionário, e podemos partir para a modelagem.
Aplicando a modelagem para a análise de concorrência
Uma das formas mais comuns de modelar séries temporais é com o modelo de médias móveis auto regressivas e integradas, mais popularmente conhecido como ARIMA. Esse modelo é calculado com base em parâmetros p,d e q, definidos a seguir:
- p: refere-se à ordem do modelo auto regressivo;
- d: refere-se ao grau de diferenciação do modelo;
- q: refere-se à ordem do modelo de média móvel.
A diferenciação de um modelo é empregada para torná-lo estacionário. Como no nosso caso já estamos trabalhando com um modelo estacionário, não há necessidade de aplicar a diferenciação.
Então, nosso modelo ARIMA transforma-se em um modelo ARMA, já que não teremos o parâmetro d.
Como próximo passo, vamos analisar a auto correlação do modelo, utilizando as funções plot_acf() e plot_pacf() da biblioteca statsmodel, que geram os gráficos a seguir.
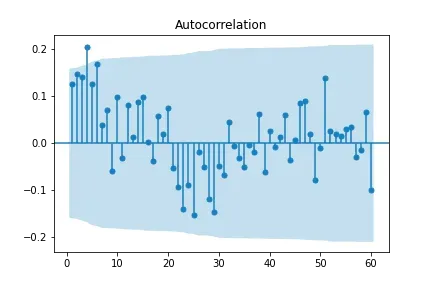
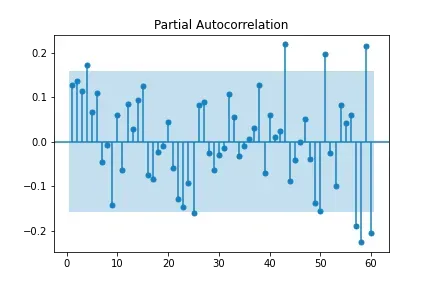
Os gráficos indicam que há correlação se existem pontos fora da região azul. Observando nosso resultado, vemos que não existe uma correlação muito discrepante entre os lags. Deste modo, também não iremos considerar o parâmetro p do modelo ARMA.
Sem os parâmetros p e d, nos resta uma modelagem por média móvel. Vamos implementá-la a seguir.
Para entendermos o efeito da média móvel, vamos aplicá-la na nossa base de teste, considerando uma média das últimas 4 semanas. A biblioteca pandas já fornece a função rolling() que facilita esse cálculo e nos permite gerar o gráfico a seguir.
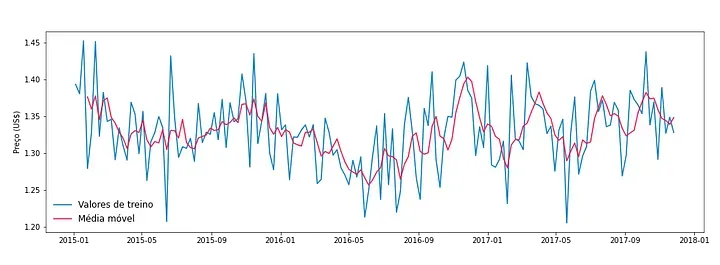
Assim como o nome já implica, obtemos valores próximos da média, mais suaves do que os originais, mas que acompanham o comportamento original.
O que realmente nos interessa, porém, é aplicar a média móvel para realizar predições dos valores das semanas seguintes. Fazemos isso criando a função moving_average() no trecho de código a seguir.
A função utiliza dados de um histórico para calcular o próximo resultado. Esse histórico é inicialmente formado pelos dados de treino e recebe os valores previstos conforme são calculados.
Como resultado, a função nos retorna os valores dos preços de abacate previstos para as próximas semanas.
No gráfico a seguir, comparamos a predição obtida com os dados da base de teste.
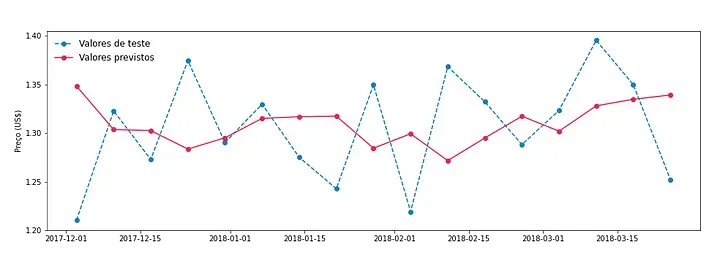
A partir da figura, podemos ver que o resultado da predição não foge muito dos valores de teste, que de fato ocorreram. Porém, é interessante validar a eficácia do modelo de uma maneira menos qualitativa.
Para isso, calcularemos o erro médio absoluto (mean absolute error — MAE) e o erro percentual absoluto médio (mean absolute percentage error — MAPE). Utilizando essas métricas, teremos maior clareza do comportamento do modelo e saberemos como podemos aplicá-lo.
Ao calcular o MAE, como o nome já indica, obtemos uma média do erro das predições obtidas, em dólares.
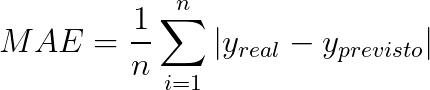
Por outro lado, calculando o MAPE obtemos uma indicação percentual do quanto nosso modelo erra:

No modelo que desenvolvemos, obtemos um MAE de aproximadamente US$ 0,05 e um MAPE de 4,15% sobre o valor real, um resultado bastante satisfatório, considerando que o preço unitário do abacate é baixo, em valores absolutos.
Fazendo uma analogia com uma possível aplicação real, vamos supor que somos vendedores de abacate e o modelo está nos mostrando dados do preço de nosso concorrente.
Caso o modelo preveja que nosso concorrente estabeleça um preço de US$1,30 na próxima semana, a partir dos erros calculados, pode-se esperar que o preço de fato esteja entre US$ 1,24 e US$ 1,35. Deste modo, ao conhecermos a possibilidade do preço aumentar, podemos fazer uma promoção e ganhar a preferência dos clientes.
É importante ressaltar que, nesta abordagem, fizemos uma análise geral de todas as localidades contidas na base de dados. Outra possibilidade seria manter a separação original e treinar diversos modelos para obter previsões de preço da concorrência por região.
Concluindo…
- Machine Learning pode ser uma forte aliada para a análise de concorrentes. Além do aspecto qualitativo desse estudo, é muito relevante termos números e métricas como as vistas nesse texto para embasar as decisões do negócio;
- Falando em predição, a análise feita aqui foi bastante simples, há muito a ser explorado no campo de séries temporais. Em especial, quanto a suas características de sazonalidade, tendência e estacionariedade, que podem tornar o trabalho de predição bastante elaborado;
- O modelo de médias móveis, ou até mesmo os modelos ARIMA e ARMA mencionados nesse texto são apenas uma fração das possibilidades. A modelagem de séries temporais é um assunto repleto de conteúdo que, quem sabe, pode até render mais publicações por aqui.
Para aprender mais sobre esse tema e assuntos relacionados, não deixe de conferir outros posts no Medium da BIX Tecnologia e nossos webinars no YouTube!
Quer saber mais sobre como seu negócio pode ser impulsionado com a ciência de dados? Entre em contato com o nosso time, ficaremos muito felizes em ajudar!
Escrito por Laura Fiorini